Kepler's investigation of what he called his "vicarious" or "substitute" hypothesis proved that the old systems of astronomy could not be made to work by simply revising them and that he needed to seek new causes and systems.

Ptolemaic System, Click to Zoom-In

Using Tycho's Brahe's observations, he built a model in the Ptolemaic style and then tested it against the same accurate and now thoroughly interrogated observations.

He sought to push the Ptolemaic system to the limit of observational accuracy and see if it would hold up in a somewhat modified form.

How does one model an orbit in the Ptolemaic style?

Kepler picked a curve which he believed would describe the orbit -- a circle, following tradition -- and then fit the "data," or the lines of sight to the planet Mars, to the curve.

Kepler stated that he made the following assumptions: He assumed that the planet moved on a circular orbit and that it swept out "equal angles in equal times" around an "equant." The "equant" and the Sun both lie on the line connecting the points of minimum and maximum speed on the orbit (the line of apsides) as prescribed by the Ptolemaic model.

How did Kepler define an orbit?

He constructed the model in the following manner: By Ptolemy’s definition, Mars moves at a uniform angular speed around the “equant,” so Kepler could match four [hypothetical] time angles that corresponded to a uniform speed for the planet (seen from the equant) with the four angles on the Zodiac (seen from the Sun) which corresponded to his actual observations. The intersection of these two sets of angles determined four unique points on a circle, and thus the circle of Mars' orbit. His procedure allowed him to locate the "equant" and the Sun spatially in the orbit, and determine the distance between them.

Click to Zoom-In

The animation below shows the approximate procedure by which Kepler matched up the angles to find the unique circle or orbit on which the two sets of angles intersected.

Kepler computed the [hypothetical] time angles by dividing the time of Mars’ orbital period (687 days) by the days between his actual observations. In his table of 12 "oppositions" Kepler called this "Mean Longitude" (See the far right column).

Kepler used a complex, repetitive geometrical procedure which was essentially the formal equivalent of "guess and check" to find the unique circle where these two sets of four angles intersected. After relating how he did it, he wrote, “If this wearisome method has filled you with loathing, it should more properly fill you with compassion for me as I have gone through it at least seventy times at the expense of a great deal of time." (Donahue translation, p. 256)

Kepler thought Ptolemy’s decision to place the center of the orbit halfway between the “equant” and the Sun was arbitrary, and his method reproduced in the animation above allowed him to experimentally locate the "equant" on the line of apsides.

Kepler obtained his model of the orbit, and then he tested it. He input the “time angles” [Mean Longitude] of the twelve observations in his table to see what “position angles” the model predicted.

The results surprised him. The actual measurements differed at most by two minutes of arc longitude from his predictions. One minute of arc is the width of a pencil lead held eight feet away. Tycho Brahe’s observation were considered accurate to within two minutes of arc, meaning his model's predictions were trustworthy to within the margin of observational error.

Kepler updated the Ptolemaic model in such a way as to place it beyond refutation, it would seem.

But Kepler did not stop there. He knew he could compute the distance from Mars to the Sun using his observations and compare it against the distance his model predicted.

Taking two observations in his table from opposite extremes of Mars' orbital plane near the line of apsides, when the vertical distance between the plane of Mars and the plane of the Earth was greatest, Kepler calculated the distance from Mars to the Sun from either extreme. The diagram below shows the trigonometry problem involved.

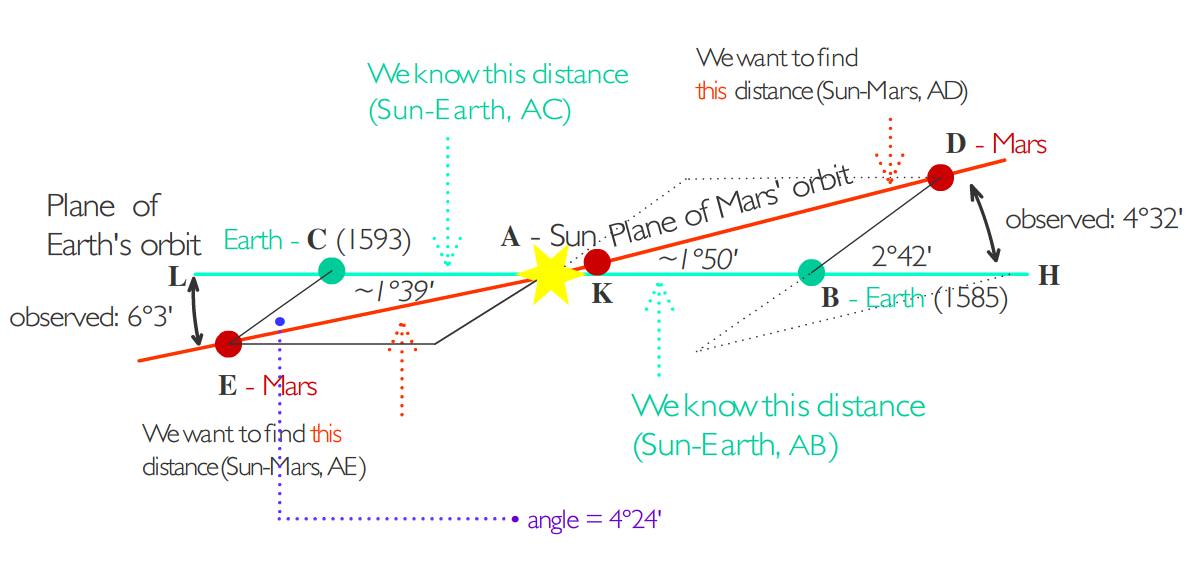
Click to Zoom-In

Kepler found that the Mars-Sun distances predicted and used by his model diverged by at least 14% and as much as 42% from the measurements he calculated with his observations.

He concluded, “Therefore something among those things we have assumed must be false. But what was assumed was: that the orbit upon which the planet moves is a perfect circle; and that there exists some unique point on the line of apsides at a fixed and constant distance from the center of the eccentric about which point Mars describes equal angles in equal times [an “equant”]. Therefore, of these, one or the other or perhaps both are false, for the observations used are not false.” (Donahue translation, p. 284)

Either the equant does not exist, or the orbit is not a circle, or both, Kepler concluded.

He altered the “Vicarious Hypothesis” model to make the Mars-Sun distances agree with the distances he computed from his observations. This placed the center of the orbit roughly halfway between the “equant” and the Sun, where Ptolemy hypothesized originally. Kepler wondered why this seemed to work.

He then computed the expected positions for his 12 observations with the "corrected" or "bisected" model and found that they differed at maximum by eight minutes from the observations. This was not a large difference. "Ptolemy," Kepler noted, "professed not to go below 10' [minutes in accuracy] in his observations."

But Kepler saw this 8' of arc discrepancy as the key to reforming astronomy:

"Since the divine benevolence has vouchsafed us Tycho Brahe, a most diligent observer, from whose observations the 8' error in this Ptolemaic computation is shown, it is fitting that we with thankful mind both acknowledge and honor this benefit of God... For if I had thought I could ignore eight minutes of longitude, in bisecting the eccentricity I would already have made enough of a correction in the [vicarious] hypothesis found in Ch. 16. Now, because they could not have been ignored, these eight minutes alone will have led the way to the reformation of all of astronomy, and have constituted the material for a great part of the present work."

(Donahue translation, p.286)