In Chapter 32 of the New Astronomy, Kepler demonstrated that the speed of the planet is proportional to its distance from the Sun. The planet moves faster when closer to the Sun, and slower when farther from it. The ratio of the speeds is the inverse of the ratio of the distances.

Kepler wondered how he could craft a dynamic speed rule that would allow him to predict how far a planet had traveled on its orbit in a given time.

He recognized that the possible positions of the planet on the orbit were “infinite [in number].” "Unless," he wrote, "we can find the sum of all of them ... we cannot say how much time has elapsed for any one of them.”

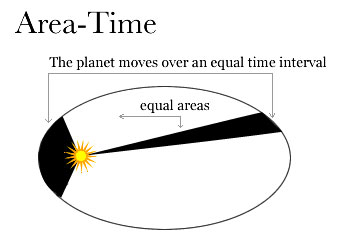
It struck him, though, that the distances from the Sun to these points were contained in the area of the orbital plane.

He remembered “that Archimedes, in seeking the ratio of the circumference to the diameter [of a circle, a ratio known as π], once thus divided a circle into an infinity of triangles—this being the hidden force of his reductio ad absurdum [his proof].”

The time required for a planet to traverse equal lengths of arc could be measured by the area of the region swept out from the Sun.

The relationship Kepler had discovered--which constituted a basic harmonic characteristic of the Solar System and of gravitation, a "law," even (now called Kepler's 2nd)--did not facilitate easy computations. Kepler could compute times and positions along the orbit to within an arbitrary degree of precision, by dividing the orbit up into, for instance, 360 parts “as if these were least particles.”

But he could not know the distance a planet had traveled for any arbitrary length of time, because the speed of the planet was changing at each moment.

Kepler did not disregard his discovery and go back to using Ptolemy's equant, however. He enjoined future geometers to find a method for measuring a planet's position at each moment while its velocity was changing at each moment.

"Anyone who ... points the way will be for me the great Apollonius," Kepler wrote.

This puzzle, referred to as the "Kepler problem," inspired mathematicians and philosophers to develop Calculus later in the 17th century to scientifically describe the "moment of change" of a system.