"If the usual popular accounts of Kepler's Mars work are anything to go by," William H. Donahue noted in a 1988 article in the Journal of the History of Astronomy, "all he had to do was plot points on the orbit by triangulation and note that they all fall on an ellipse with one focus at the Sun." Donahue continues, "To the few scholars who have actually studied Kepler's New Astronomy (1609), however, it is clear that the points plotted do not fall so neatly."

Donahue notes, that Kepler "could not possibly have used the triangulation to determine the orbit, because the procedure of triangulation was too imprecise." Rather, Kepler used the triangulation "only as a guide to his theorizing."

Kepler had discovered that the orbit of Mars could not be a circle but rather some kind of oval shape. We discuss his geometrical demonstration on the next page, "Mars' Orbit is Not a Circle."

After ruling out various possibilities using a triangulation procedure that employed the physically false but accurately predictive "Vicarious Hypothesis" to generate orbital elements, Kepler postulated the idea of an ellipse as the shape of the orbit. He then used the elliptical model to generate a table of planetary positions, and tried to make it look as if he had arrived at these results by triangulation. We might criticize him for this method, but why did Kepler get it right?

In order to understand the phenomena of refraction in Kepler's study on Optics, he researched the writings on conic sections by the ancient Greek geometer and astronomer, Apollonius of Perga (c. 240 BCE-c.190 BCE). The idea that the circle, the ellipse, the parabola and the hyperbola are all generated by a continuous process of rotating the plane that cuts a cone, interested the astronomer.

Furthermore, Kepler found that the difficulties which arose in using area to calculate the position of the planet on a circular orbit (due to the fact that the circular model was not centered on the Sun) vanished with the elliptical model.

In the New Astronomy Kepler noted a wide variety of unique, harmonic properties of the ellipse, such as those illustrated below, as part of an effort to make an argument for the shape as the form of the orbit based on a priori criteria.

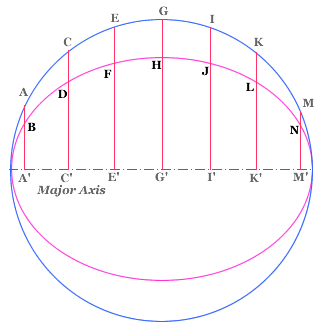
An ellipse inscribed in a circle divides lines drawn from its major axis to the circle proportionally. Point "B" divides line AA' in the same proportion as point "D" divides line CC', and so on.

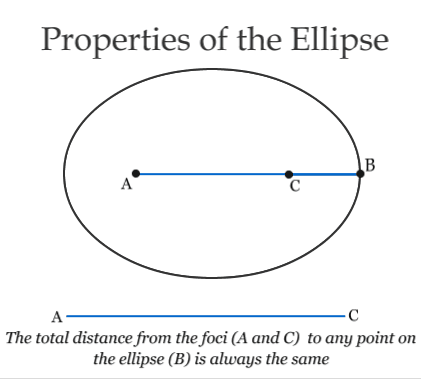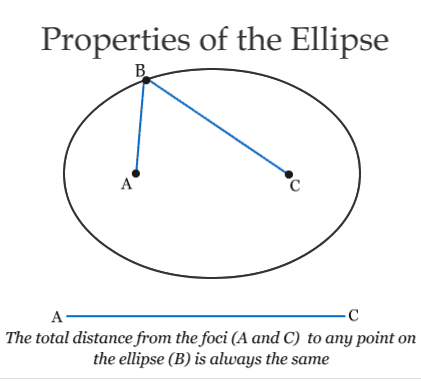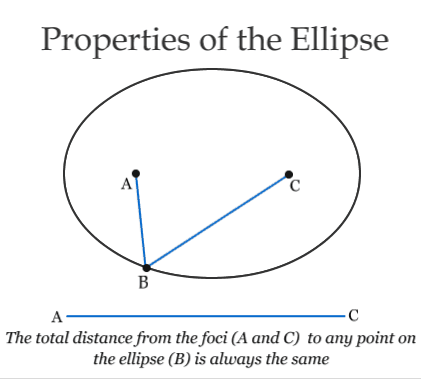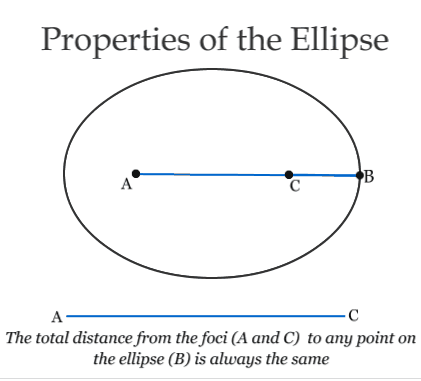
Kepler determined that the Sun must lie at one of the two foci of the ellipse (see the animation below). Today, Kepler's "First Law" is the idea that a planetary orbit is an ellipse lying in a plane with the Sun at one of the foci.