Kepler's essay, "On the Six-Cornered Snowflake," is considered to be the first work that analyzes and describes the structure of crystals.

In naming his essay, Kepler consciously played with words and made a pun with the word nix: In Latin, the language in which he composed the essay, the word means "snowflake," but in Low German, Kepler's native tongue, it means "nothing." At its core, the essay functions as a meditation on the nature of substance: if a snowflake, crafted of water vapor, melts momentarily, is it anything at all?

Kepler worked as the imperial astronomer for Emperor Rudolph II, who had neglected to pay the scientist's salary for some time. Lacking the necessary funds to buy an appropriate Christmas gift for a friend, Kepler decided to write the essay on the snowflake. After all, he asked rhetorically, what do astronomers and mathematicians "who have Nothing and receive Nothing" have to give, but Nothing?

As part of his meditation on "nothing" (nix), Kepler considers the smallest particle of dust and asks, is this nothing? No, he decided, it would be too much to give. Dust, after all, settles on the interior beams of houses where it stays for a long time. What about water? Indeed, he could surely insult someone by giving him only a tiny drop of water for Christmas.

But Kepler surmised that a particle of dust and the tiny drop of water did indeed represent something, rather than nothing.

When a snowflake alighted on Kepler’s coat as he crossed the Charles Bridge in Prague, he marveled at its perfect six-cornered symmetry. In his essay Kepler recounted thinking that the snowflake would be the perfect Christmas gift, “since it comes down from heaven and looks like a star.”

But why, he asks, do single snowflakes, before they become entangled with other snowflakes, always fall with six corners? Why do snowflakes not fall with five corners or with seven?

Perhaps it is because the hexagon, he surmised, is one of only three shapes along with the triangle and the square that fill up a plane without leaving spaces.

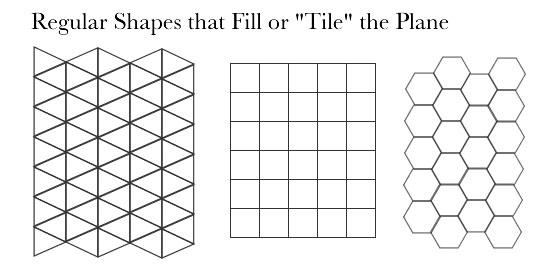
He looked to the beehive as an example, since bees also make their houses "on a six-cornered plan.”

The bees share six walls with their neighbors around the circumference of their cells. Yet Kepler uncovered something unexpected. The interior rear walls of the bees' cells are not flat as one might expect (see below) but rather adjoin four neighbors' walls.

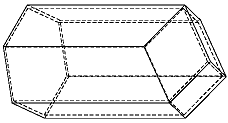
The cells are thus off-set from each other, nestling together such that each bee's cell adjoins those of four neighbors on the back end, as well as six neighbors around the circumference.

The shapes formed where the rear walls of the cells meet are called rhombi by geometers, Kepler noted.

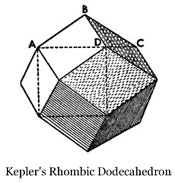
This observation gave Kepler an idea. He wondered if he could construct a solid figure, similar to the Platonic and Archimedean solids, made out of nothing but rhombi. He explained that he found one (see the illustration at the right), bounded by twelve rhombi that shares the property in common with the cube that it can fill the whole three dimensional space while leaving no area empty, in the same manner that the hexagon, square, and triangle fill the plane surface.

Kepler observed that the seeds of pomegranates are pressed together inside the fruit in approximately this kind of shape.

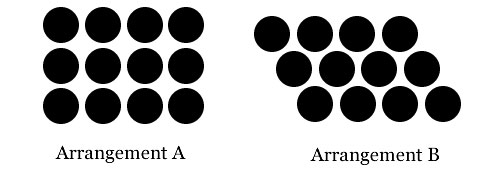
He surmised that this packing arrangement is likely the most efficient way for spherical seeds to fill space as they expand. If spherical pellets are allowed to roll freely they will align in the arrangement "B" (shown below), and squeezing them together with even pressure will produce shapes corresponding to Kepler's rhombic dodecahedron.

However, Kepler observed that if round balls are aligned at right angles to each other inside a container, applying even pressure would produce cubes.

But the rhomboid packing "will be the tightest possible," Kepler conjectured , "so that in no other arrangement could more pellets be stuffed into the same container.”

“In honeycombs the reason is different,” he wrote. The arrangement of cells pressed tail-to-tail allows the bees to easily exit the hive.

Here, Kepler searched for a reason, a "formative principle" to explain the structures he observed. The architecture of the beehive maximizes the number of walls each bee shares with its neighbor, allowing bees to collaborate in constructing the shared walls of a cell. Kepler quoted the Roman scholar Virgil (70-18 BCE), saying “they hold the houses of their city in common.” This necessity, then, underlies the "formative principle" of the beehive, just as the dense-packing principle explains the shape of a pomegranate seed.

What, he asked, is the "formative principle" of the snowflake?

Proceeding through a variety of possible causes, he considered the manner in which heat retreats from water vapor as the possible architect of the six-cornered shape. But is the shape imprinted on the snowflake from outside or does it arises from intrinsic properties of the vapor? Kepler knew the shape of crystals found in mines appears to vary with impurities found in the material. Metallic sulfates tend to produce rhomboid or cubic crystals, while other minerals form icosahedral crystals. (An icosahedron is a polyhedron having 20 faces.) Does some property of water vapor, or impurities in it account for its six-cornered shape, or must an external cause be sought?

And why is the snowflake flat? Why does it not assume a three dimensional shape?

This last question in particular puzzled Kepler.

“I have not yet got to the bottom of this,” he wrote and added: “Nothing to follow.”

Note: The most recent edition of Kepler's "The Six-Cornered Snowflake" appeared in 1966 from Oxford's Clarendon Press, translated by Colin Hardie (available in libraries). It is a fine edition with the original Latin on the facing page and an introductory essay on the history of crystallography.

Image Credit: Blue snowflakes at top by Elvis Santana.