Geometry has two great treasures; one is the Theorem of Pythagoras; the other, the division of a line into extreme and mean ratio. The first we may compare to a measure of gold, the second we may name a precious jewel.--Johannes Kepler
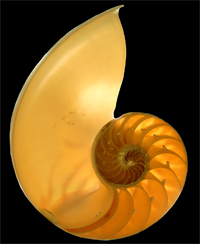
In a paragraph towards the end of his 1611 essay On the Six Cornered Snowflake Kepler mentions the “Divine Proportion" (Golden section) and the "fibonacci sequence” in practically the same breath as flowers and pentagons.
"It is in the likeness of this self-developing series that the faculty of propagation is, in my opinion, manifest: and so in a flower the authentic flag of this faculty is shown, the pentagon." (emphasis added)
What does Kepler mean here?
First, we examine the nature of the logarithmic spiral, for reasons that will become evident below.
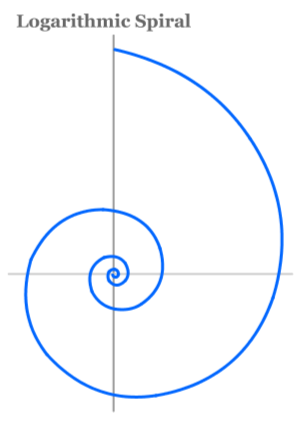
The 17th century mathematician Jakob Bernoulli named the figure at right the Spira mirabilis or "miraculous spiral" and assigned it the following motto: "Eadem mutato resurgo" ("although changed, I rise again the same").
The logarithmic spiral does not change its shape as its size increases. This feature is known as self-similarity. If we could zoom into the coils of the figure near the origin and enlarge them, they would fit precisely on the larger spiral.
The spiral has another extraordinary property: turning by equal angles increases the distance from the pole to the spiral by equal ratios.
What are fibonacci numbers?
In the "fibonacci sequence," referenced by Kepler, each number is the sum of the two proceeding numbers (1, 2, 3, 5, 8, 13, 21...). Therefore, the sequence can be called a "self-developing" series.
Interestingly, dividing two adjacent fibonacci number (8/5 or 21/13, for example) by each other produces increasingly precise approximation of the "Divine Proportion," which we will explore below, as the numbers grow larger.

Why does Kepler mention flowers?
Scientists, beginning with Leonardo da Vinci, observed that the displacement of leaves around a stem occurs in patterns defined by the fibonacci series.
This phenomenon is known as "philotaxis."

In the case of roses an angle that is congruent to 360 degrees by the Divine Proportion (137.5 degrees) separates the petals from each other.

In other plants the number of leaves measured around a screw-type displacement between one leaf and the leaf directly above it, and the number of rows separating the two are both fibonacci numbers.
The same phenomenon occurs in pine cones and the hearts of sunflowers.
How is the Divine Proportion related to the pentagon?
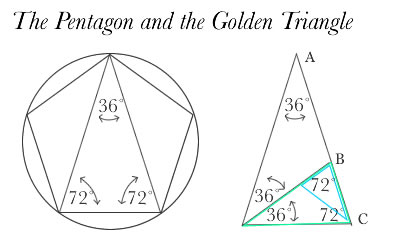
The Divine Proportion plays an essential role in the construction of the pentagon and five-fold symmetry.
To see this, examine the diagonals in a pentagon. The ratio of the diagonal to the side of a pentagon is the Divine Proportion. Moreover, the diagonals create an isosceles triangle (where two of the three sides are equal) with angles of 72 degrees and 36 degrees. This triangle can be reproduced inside itself to infinity (in a "self-developing" manner), as shown below.
In constructions of tiled pentagons, every segment is smaller than its predecessor by a factor equal to the Divine Proportion.
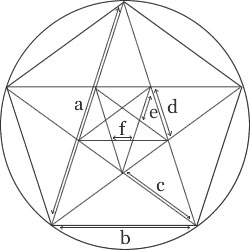
The ratio of "a" to "b" is the Divine Proportion, the ratio of "b" to "c" is the Divine Proportion, and so on.
How does this relate to the logarithmic spiral?
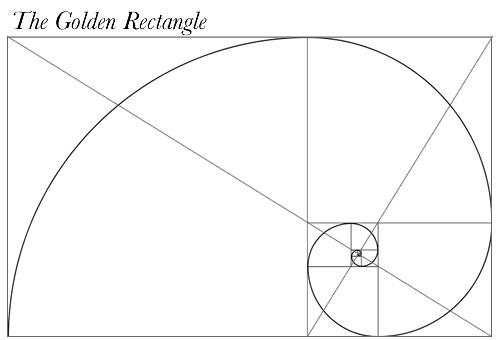
In a rectangle where the ratio of the larger side to the smaller one is the Divine Proportion, the ratio of the sides of the "daughter rectangles" will still conform to the Divine Proportion when squares are cut from the original rectangle. Connecting the points where this series of "whirling squares" divides the sides will generate a logarithmic spiral that coils inward.
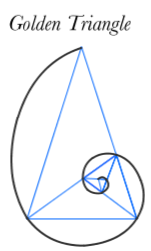
Similarly, connecting the vertices of the nested "Golden Triangles" inside the pentagon will produce the logarithmic spiral as well.
What is the "extreme and mean ratio?"
Euclid defines the "extreme and mean ratio," or "Divine Proportion," as the following relationship: When a line is divided such that the smaller section of the line (BC) is related to the larger section of the line (AC) in the same ratio as the larger section is related to the whole line (AC), then the line is divided in the Divine Proportion.
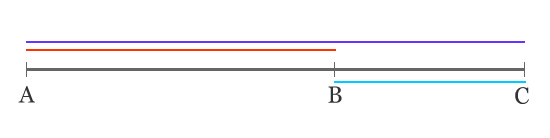
Move the slider to move point B:
| Whole Line length |
Shorter Segment length |
Longer Segment length |
|---|---|---|
| AC | ||
| Ratio of smaller section to the larger section | ||
| Ratio of larger section to the whole | ||
| Result: | ||

+ Photo Credits: Chambered nautilus by Peter Werner. Lotus flower by Sanja Moharic Hehet.


